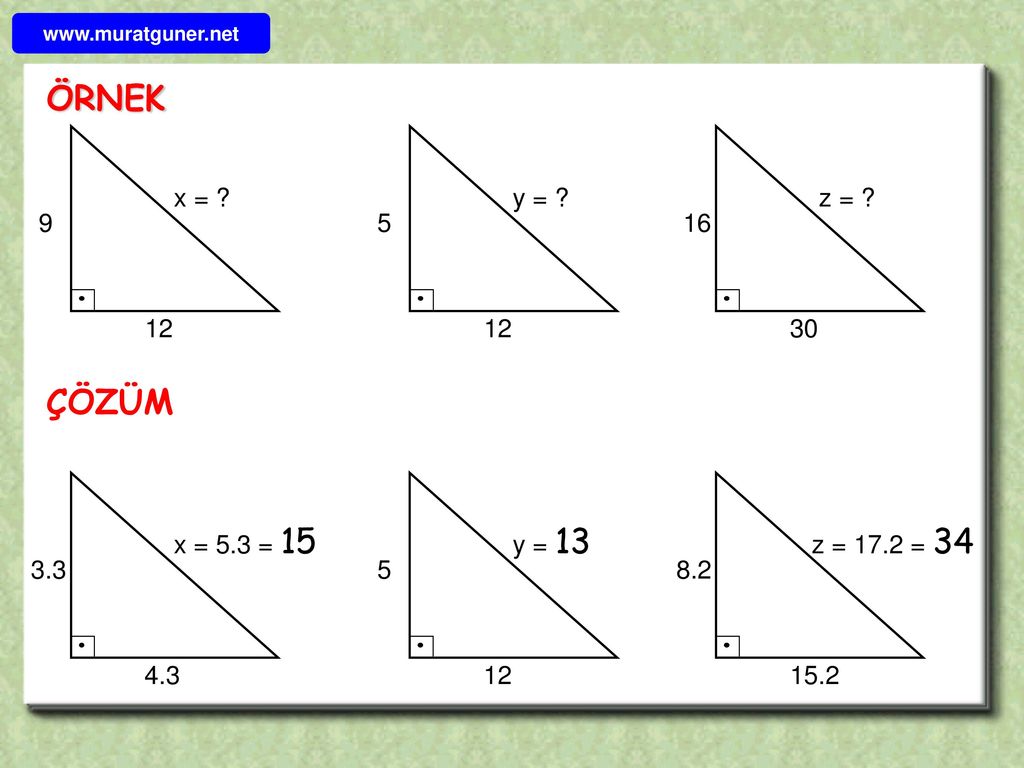
DİK ÜÇGEN 16 15 75 90 ÜÇGENİ kaydeden Mustafa YAZAGAN 62 Kişisel Gelişim Geometri Psikoloji Science Harfler Eğitim Banyo Daha fazla bilgi Bunun gibi daha fazlası15 75 90 ÜÇGENİ VE ÖZELLİKLERİ ÖKLİT BAĞINTILARI HAKKIMIZDA Bu sayfada yer alan bilgilerin her hakkı, aksi ayrıca belirtilmediği sürece TestDefteriCom'a aittir Sitemizde yer alan dosya ve içeriklerin telif hakları dosya ve içerik gönderenlerin kendilerine veya yetki verdikleri kişilere aittir Sitemiz hiç bir şekilde12 A B C E 75 15 H 15 x EH = x uzunluğudur Buradan AB = 4 EH olduğundan, 12 = 4 x x = 3 br bulunur Cevap A'dır (vii)(30 30 1 ) ÜÇGENİ A B C 30 30 1
Dik Ve Ozel Ucgenler 1
15 75 90 üçgeni kenar özellikleri
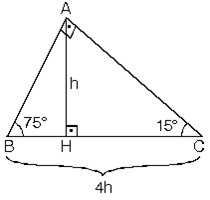
15 75 90 üçgeni kenar özellikleri- özel bir dik üçgendir 90 derecelik açının karşısında hipotenüs bunulunur Bu 90 derecelik açının olduğu yerden hipotenüse indirilecek dik (yani yükseklik) h olursa hipotenüs de 4h olacaktır 5 ayrıca 75 ten uzatılacak kol ile 15 15 eş üçgeni ve 30 60 90 dik üçgeniİkizkenar Üçgenler İkizkenar Üçgenler konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruz




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu
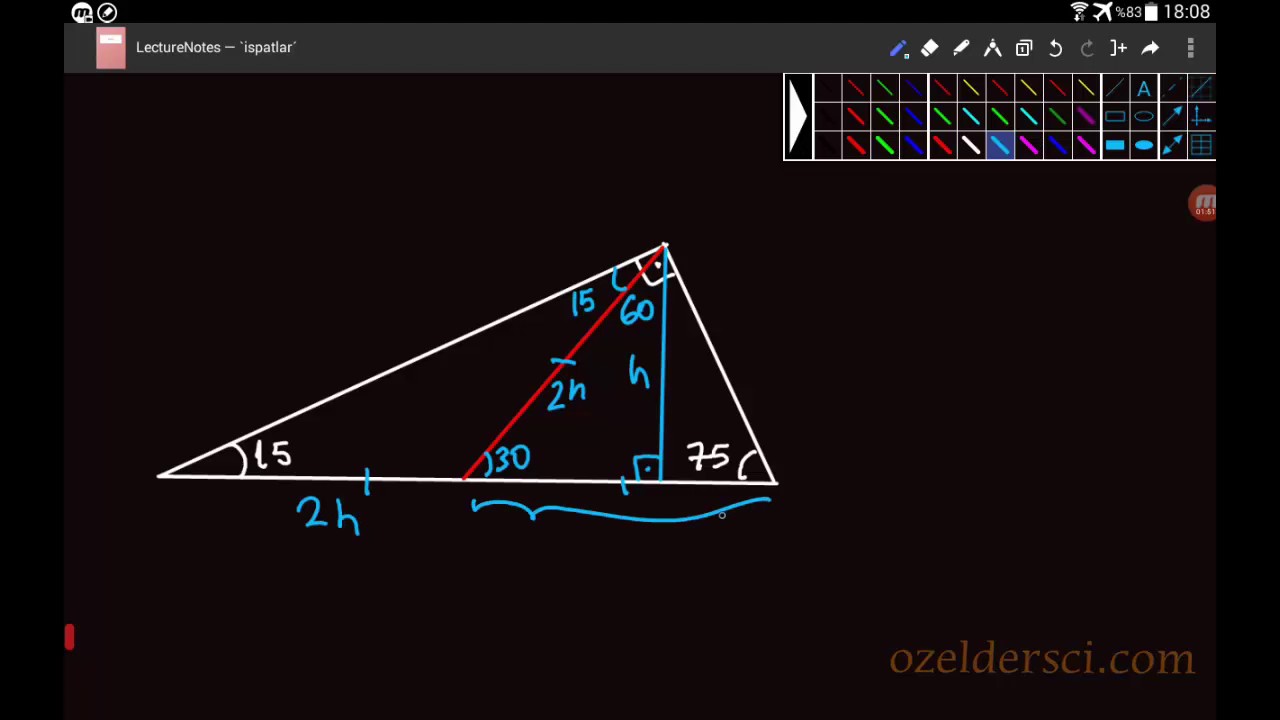
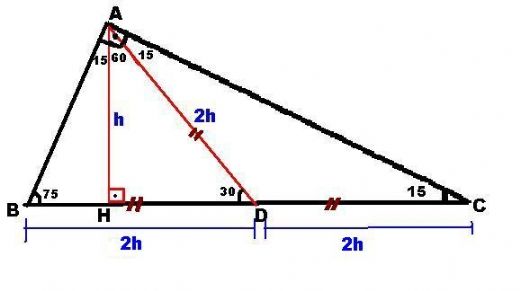
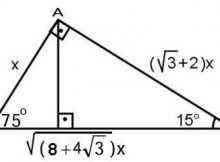
Üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu üçgende hipotenüse indirilen dikme, hipotenüsün katıdır Üçgeni (h4h) İSPAT üçgeninde hipotenüse indirilen yüksekliğe h diyelim Daha Sonra Süper üçlüyü kullanmak için hipotenüsü iki eşit parçaya bölecek kenarortayı çizelim 3 adet üçgenimiz oluştu () () (0) 30⁰'nin karşısına h dediğimiz zaman 90⁰'nin karşısına 2h1 Bir Üçgenin iç açılarının toplamı 180° dış açılarının toplamı 360°'dir 2 Üçgende bir dış açı, kendisine komşu olmayan iki iç açının toplamına eşittir 3 Bir dik üçgenin dik kenarlarına 'a' ve 'b' dersek hipotenüs'ün karesi bu kenarların uzunluklarının karelerinin toplamına
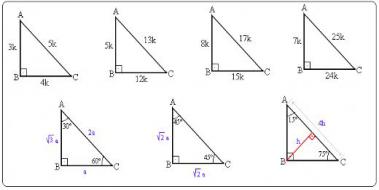
4 (30° – 60° – 90°) Üçgeni 5 (30° 30° 1°) Üçgeni 6 (15° 75° 90°) Üçgeni ÖKLİT BAĞINTILARI Sponsorlu Bağlantılar Dik açılı üçgen, iç açılarından biri 90° olan üçgendir Çemberde çapı gören çevre açı 90°'dir Bir dik üçgende kenarlar arasında a2 = b2 c2 bağıntısı vardırQuote Orijinalden alıntı brknzbz üçgeninde şu bağıntılar vardır 1 (kök31)k (kök31)k (2kök2)k sırasıyla derecelerin karşılarındaki kenarların aralarındaki bağıntıdır bu 2 15 derecenin hemen yanına doğru bir doğru parçası indirerek ikizkenar üçgen oluşturup (1515 derece şeklinde) küçük bir 0 ve üçgeni oluşturmakBu ders notumuzda Geometri dersinin Özel Üçgenler başlığı altında;
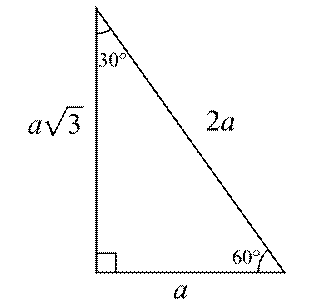
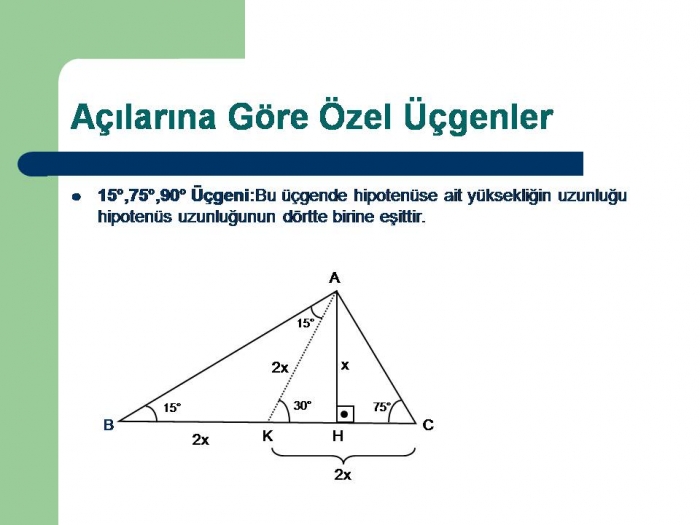
EN İYİ CEVABI Safi verdi 22,5 67,5 90 üçgeninin ve üçgeninin özelliklerini Açılarından ötürü özel dik üçgenlerdir ve özellikleri şöyledir Sponsorlu Bağlantılar 1 22,567,590 Üçgeni Bu üçgende ise 22,5°'lik açının karşısındaki dik kenar 1 cm ise, 67,5 cm'lik kenarın karşısındaki kenar cm olur5 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur 15 75 90 üçgeni 2 ayrı çözüm yöntemi bulunur bunlardan bir tanesi 75 derecelik açıyı 30 ve 45 olarak, diğeri de 15 ve 60 olarak bölmektir 30 ve 45 olar



15 75 90 Ucgeni Ozellikleri




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali
Bu sayede iki adet eş 30 60 90 üçgeni oluşturursunuz ki bunun bütün özelliklerinden yararlanabilirsiniz 0 Paylaş admin 116 İçerik 10 Cevap Önceki 0 Tam Sayı Mıdır ?7 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar a 3 olur 8 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olurKÜME EĞİTİMBUTİK DERSANE ANKARAİLKER ÇORSUZ




15 45 1 Ozel Ucgeni Var Mi Varsa Kurali Nedir Eodev Com



Dik Ucgende Trigonometrik Oranlar
15 75 90 üçgeni özelliklerinin ispatını gösteriyoruz, videomuzu izleyerek öğrenebilirsiniz SIFIRDAN MATEMATİK ÖĞRENİN İspat videolarımız ve dolayısı ile işin manasını, aslını, neyin nerden geldiğini anlatan ve bilginin kalıcı olmasını sağlayan videolarımız devam ediyor 15° 75° 90° üçgeni, Özel bir üçgendir Matematikte özel kavramı; 75 dereceyi 1560 derece olacak şekilde ayıran bir kenar çizip karşı dik kenar ile birleştirirsek, bir tarafta ikizkenar üçgen diğer tarafta üçgeni oluşur ve kenar uzunlukları arasındaki bağıntı ezberlenmemiş olur dik kenarlar arasındaki bağıntıyı hatırlayacak olursak, 15 in karşısındaki kenar "a" ise 75 in




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ucgeni Ozellikleri Ve Sorulari



Ozel Ucgenler Konu Anlatimi
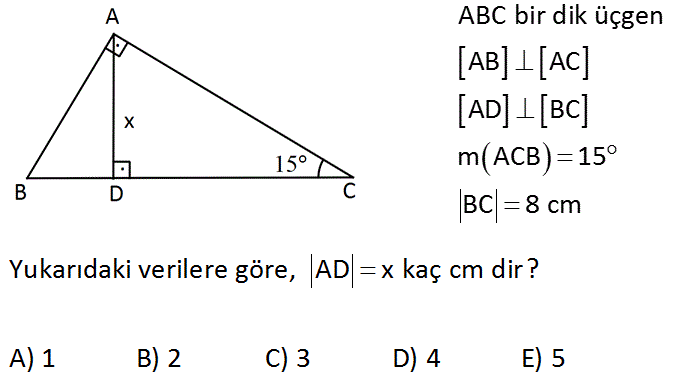
15 75 90 Üçgeni Özellikleri Sorularda bir üçgene, bir dikdörtgene ya da herhangi bir çokgene dikme indirerek veya bir çizgi çekerek karşınıza 15 75 90 üçgeninin çıkmasını sağlayabilirsiniz Bu üçgeni bulduktan sonra aşağıdaki kuralları aklınızdan çıkarmamanız gerekir Dik üçgendir Bu üçgenin iki darA) 6 B) 7 C) 8 D) 10 E) 12 wwwmatematikkolaynet Çözüm BCD üçgeni bir 30 60 90 üçgenidir 30 nin karşısı 12 ise 90 nin karşısı bunun iki katı yani 24 cm dir ABC üçgeni bir üçgenidir Bu üçgenin 1 yüksekliği, tabanın 'ü dür Bu sebeple; 15 75 90 üçgeni özellikleri Bir dik üçgendir İki dar açısının toplamı dik açısını vermektedir İki dar açı karşısındaki dar kenarlarının toplamı her daim dik açının karşısındaki geniş kenar uzunluğunu vermek zorundadır İki dar açının oranı 1/5
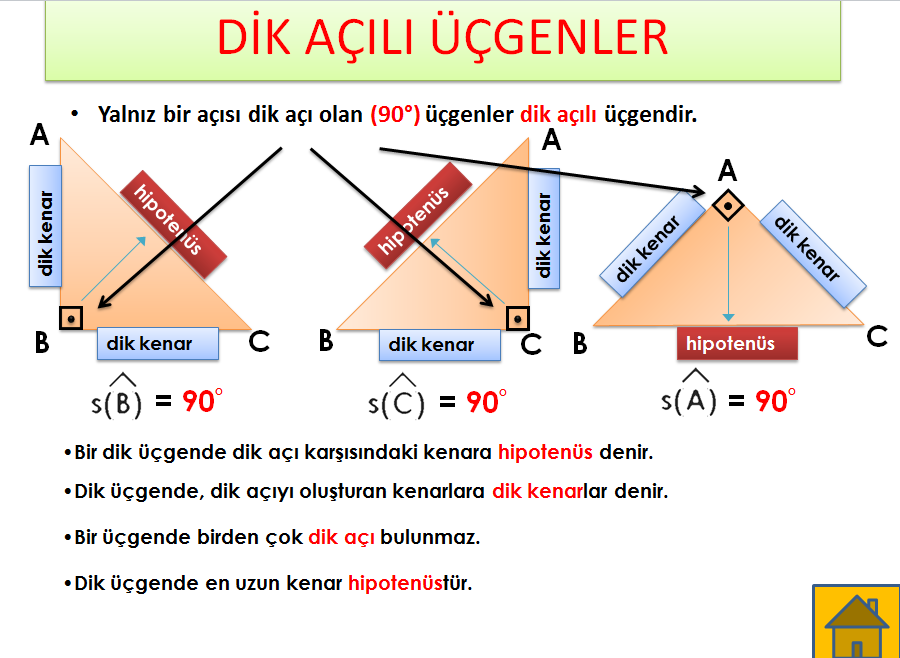



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




30 30 1 Ucgeni Not Bu
Dik üçgende dik kenarların uzunluklarının kareleri toplamı4 24 x 6 cm bu 4 luruz 53 15 75 90 üçgeni özelliklerinin ispatıDaha fazla ispat için http//wwwozelderscicom/matematikformullerininteoremlerininhtmlSitemizi ziyaret e
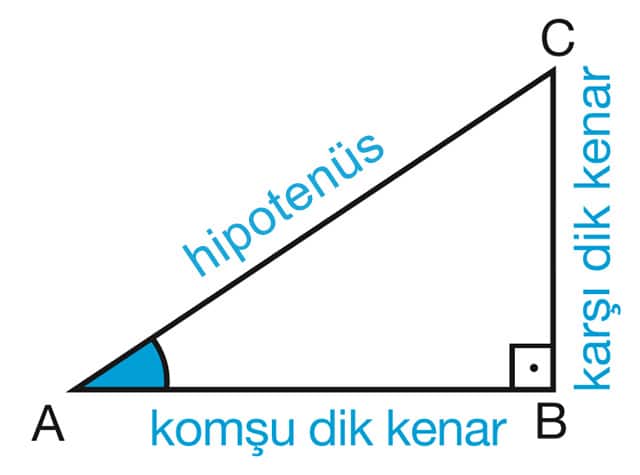



Trigonometri Dik Ucgenlerdeki Trigonometrik Oranlar Matematikciler Com




2 Kok 5 3 Ucgeni
Geometrideki özel üçgenlerden biri de 15 75 90 üçgeni dediğimiz özel üçgendir Bu üçgen karşımıza diğer özel üçgenler kadar yaygın çıkmasa da üçgenini bilmek bize geometride birçok yerde fayda sağlayacaktır Çünkü bu üçgen türü karşımıza tek başına çıkmasa dahi soru içerisinde çıkabilmektedir 15 75 90 üçgeni ile ilgili özellikleri üçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar cm olur İspatı ise 22,567,590 üçgenindeki gibidir Soru çözümlemelerinde dikkat etmeniz gereken en önemli konu 15 75 90 Özel Üçgeni kenar uzunluklarını biliyor olmanız gerektiğidir 15 75 90 Üçgeni Özellikleri 15 75 90 Üçgeninde Kenarların Oranı 15 75 90 üçgeninde kenarlar arasında belirli bir oran bulunması zorunluluğu vardır




Www Notbu Net Wp Content Uploads 19 02 3 4 5
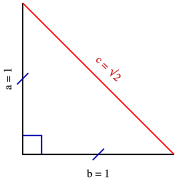



Dik Ucgen Vikipedi
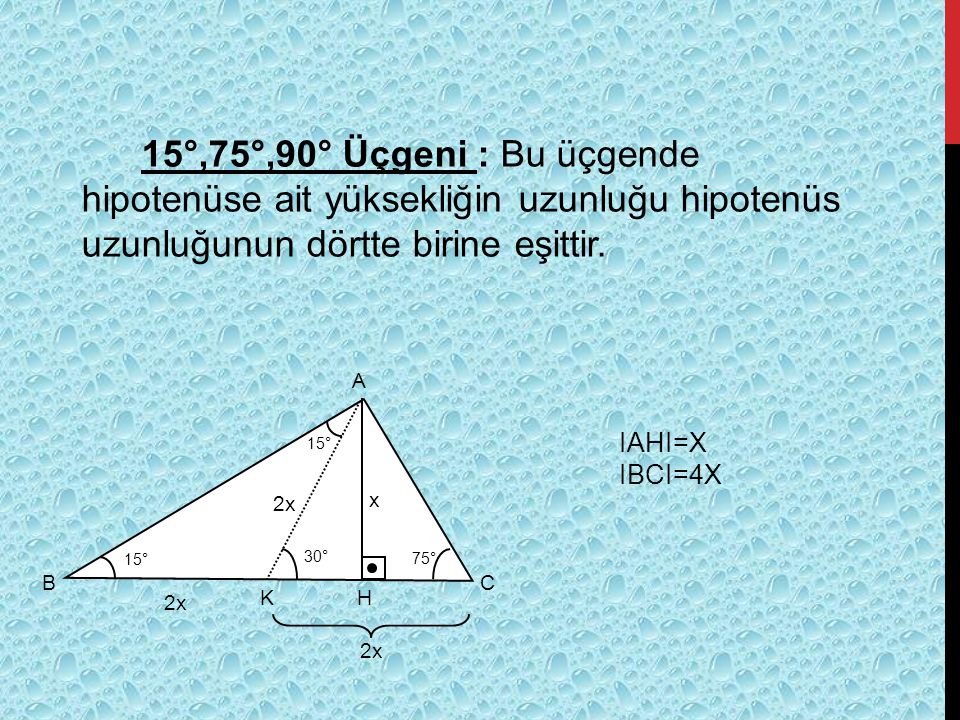
15 75 90 Üçgeni (15°, 75°, 90°) dik üçgeninde hipotenüsü ait yükseklik hipotenüsün dörtte birine eşittir 30 30 1 Üçgeni 30 – 30 – 1 ikizkenar üçgeni iki adet 30 – 60 – 90 dik üçgeninden oluşur 1 0 'nin karşısındaki kenar ikiz kenarların √3 katına eşittir 15 – 75 – 90 DİK ÜÇGENİ Eğer bir 15 75 90 üçgeni düşünecek olursak;Dik Üçgen, Pisagor Bağıntısı, Özel Dik Üçgenler, İkizkenar dik üçgen, (30° – 60° – 90°) Üçgeni, (30° – 30° – 1°) Üçgeni, (15° – 75° – 90°) Üçgeni, Öklit Bağıntıları, İkizkenar Üçgen, Eşkenar Üçgen vb içerikler hakkında detaylı bilgileri bulabilirsiniz




ラブリー75 15 90 Ucgeni 最高のぬりえ




Ucgende Acilar
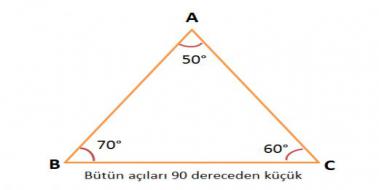
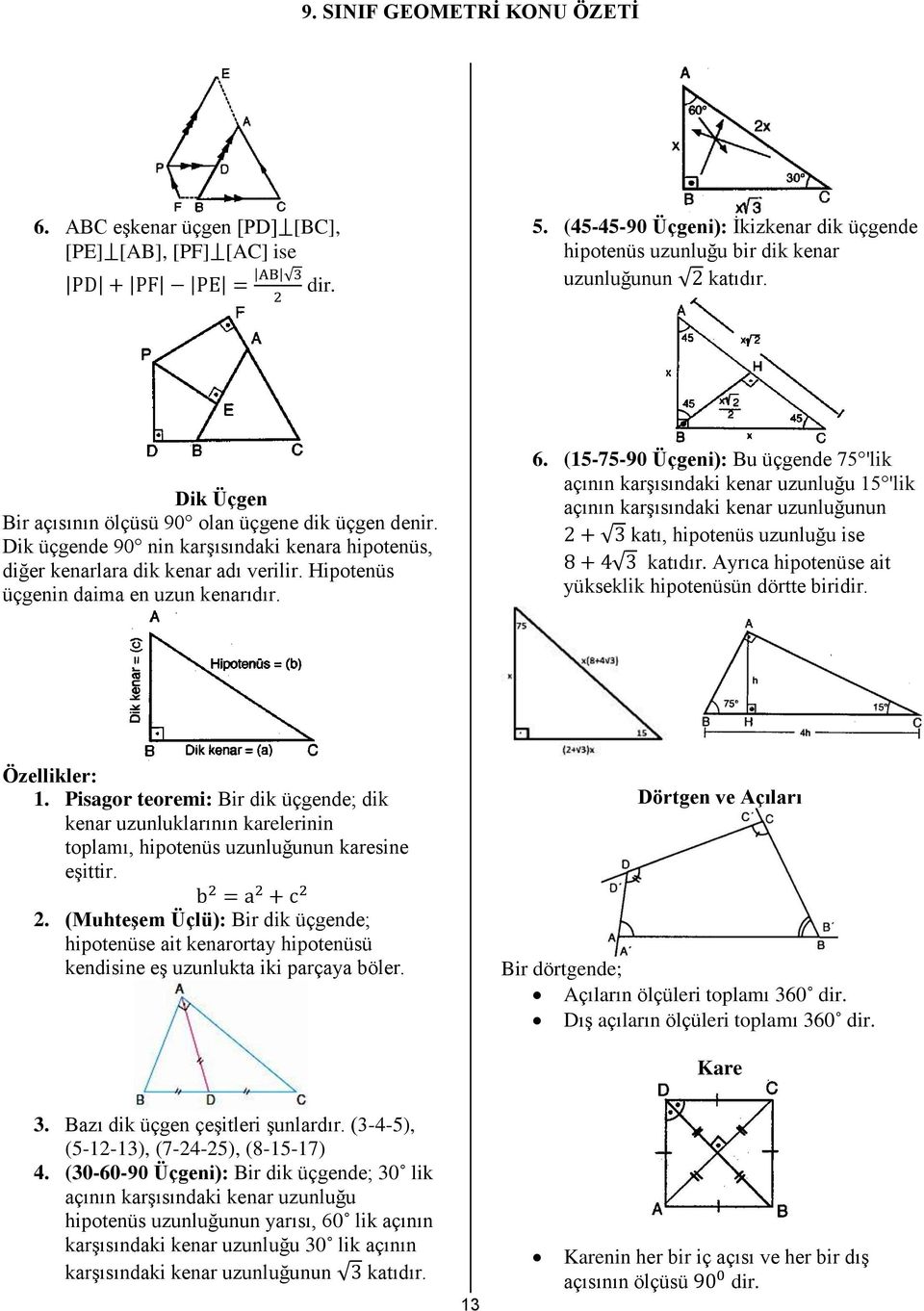
(A açısı = 90 (B açısı = 75 (C açısı = 15 açıları ise uzunlukları şu kural doğrultusunda olmalıdır15 75 90 Üçgeni Özellikleri ve Kuralları Geometri dersi için özel üçgenlerin büyük önemi bulunmaktadır Özellikle bu tür üçgenlerin özellikleri bilindiğinde pek çok soru çok rahat bir şekilde çözülmektedir 15 75 90 üçgeni de bu özel üçgenler arasında özellikle bilinmesi gereken üçgenler arasında yer almaktadırDik Üçgenin Özellikleri Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m (A) = 90° BC kenarı hipotenüs AB ve AC kenarları dik kenarlardır




Nature And Genesis Of Potassic High Basr Granitoids Associated With Syn Convergent Extension In Nw Turkey Sciencedirect




Pdf Influence Of Foreign Ions On The Crystal Structure Of Batio3
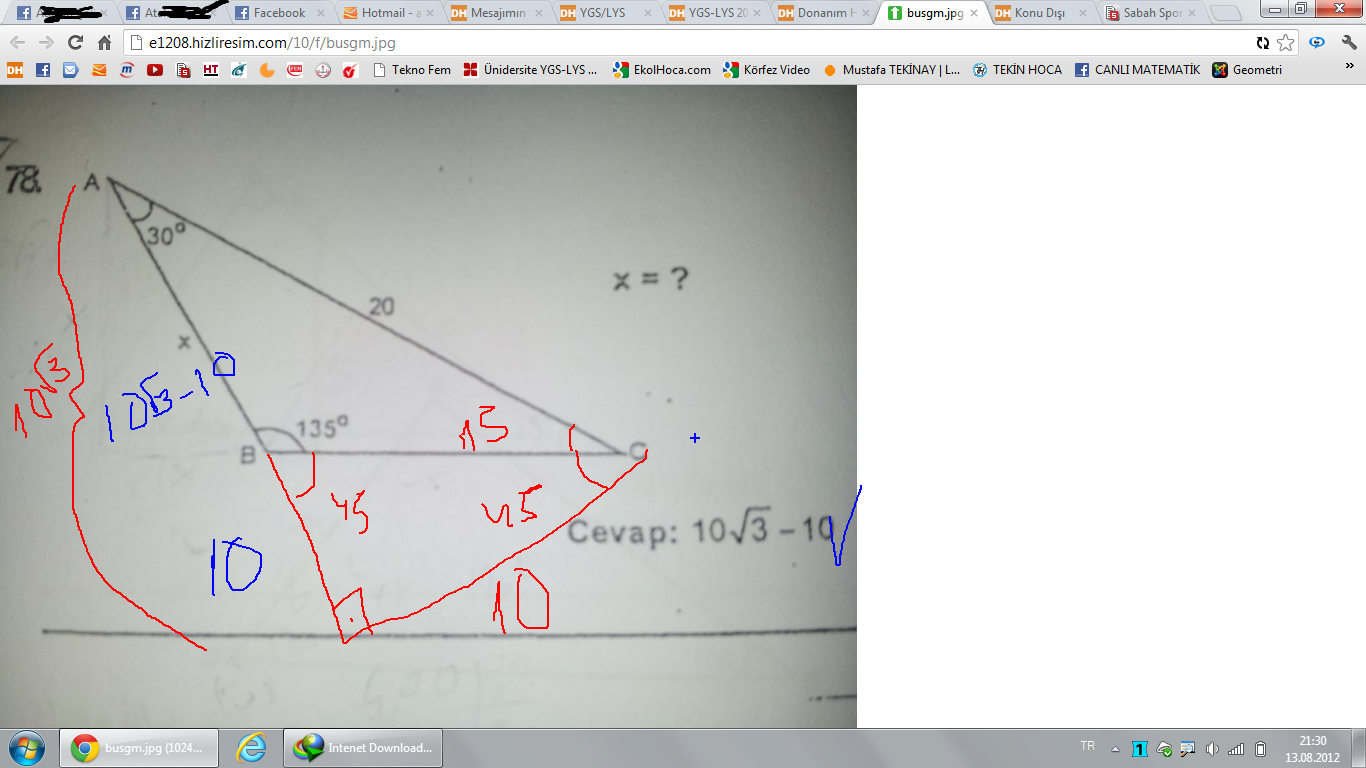
75 60 30 75 75 5 5 10 DC = 5 cm ise AB = 5 cm dir Soruda ölçüleri bilinen açıları şekilde yerine yazdığımızda ABL (30 60 90 ) üçgeni ve ALD ikizkenar üçgen olduğu açıktır ABL üçgeninde 30 yi gören AB = 5 cm ise hipotenüsün uzunluğu AL = 10 cm olurSonraki 15 75 90 Üçgeni Özellikleri ve Kuralı 1575 90 Üçgeni Bu üçgende hipotenüsün yüksekliğine x dediğimiz zaman hipotenüsün uzunluğu bu ölçünün 4 katı yanı 4x olmaktadır İkizkenar Üçgen Özellikleri
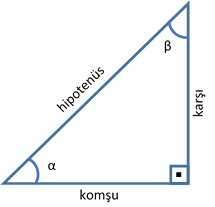



Dik Ucgende Trigonometrik Hesaplamalar



Ozel Dik Ucgenler Delinetciler Portal
22,5 67,5 90 üçgeninin ve üçgeninin özelliklerini Açılarından ötürü özel dik üçgenlerdir ve özellikleri şöyledir 1 22,567,590 Üçgeni Bu üçgende ise 22,5°'lik açının karşısındaki dik kenar 1 cm ise, 67,5 cm'lik kenarın karşısındaki kenar cm olur İspatı ise 67,5°'lik açıyı 45° ve 22,5Teoremin kendine has özelliklerinin olmasıdır Bu özellikler başka hiç bir teoremde yada cisimde bulunmamasıdır En önemlisi de teoremi çözebilmek için bazı kuralların ve formüllerin kullanmas 15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğer



15 75 90 Ucgeni




15 75 90 Ozel Ucgeni Oluyor Ama Ben Sadece O Ucgenin Yukseklik Le Ilgili Ozelligini Biliyorum Baska Eodev Com
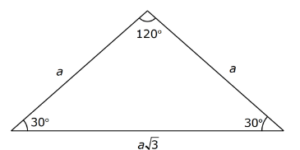
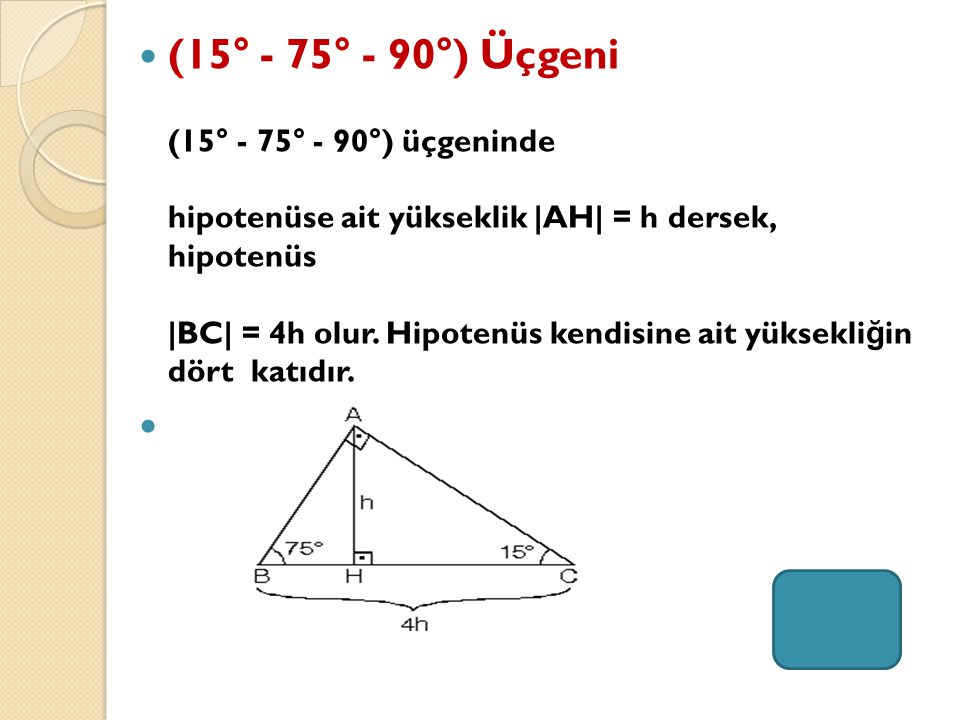
15 75 90 üçgeninde 90°'lik açının karşısındaki kenarın (hipotenüsün) uzunluğu (√2 √6)k 'dir 15 75 90 Üçgeni Özellikleri 1 15 75 90 Üçgeninin kenar uzunluklarının toplamı (√2 √3 √6 √9)k 'dir Dar Açılı Üçgen Özellikleri Dar açılı üçgenlerin hiç bir iç açısı 90 derece olamaz Eğer doksan derece varsa bu dik açılı bir üçgendir Diğer iç açılarının 90 dereceden küçük olması üçgenin dar açılı olduğunu göstermez Örneğin açıları 30,60,905 (30° 30° 1°) Üçgeni (30° 30° 1°) üçgeninde 30° lik açıların karşılarındaki kenarlara a dersek 1° lik açının karşısındaki kenar aÖ3 olur 6 (15° 75° 90°) Üçgeni (15° 75° 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur




Zlltb9utgct6pm



45 45 90 Ucgeni Matematikce
7 24 25 ÜÇGENİ ÖZELLİKLERİ Bu üçgen sadece 7 24 25 olarak değil 14 48 50/ 21 72 75/ 28 96 100 olarak da karşımıza çıkmaktadır Uzunluğu 25 ile orantılı olan kenarı gören açının ölçüsü ise 90 derecedir 7 24 24 ÜÇGENİ AÇILARI 15 75 90 ÜÇGENİ ÖZELLİKLERİ 15 75 90 üçgeni bir dik üçgendir İç açıları toplamı 180 derecedir Dış açıları toplamı 360 derecedir İki dar açısının toplamı diğer açının ölçüsünü vermektedir İki dar açının birbirine oranı 1/5 olmalıdır Hipotenüse ait yükseklik hipotenüs uzunluğunun 4'te 1'idirH = 7,75 cm İkinci alıştırma Ölçekleri ABC, hangi ölçüleri şunlardır AB segmenti = 25 m Segment BC = 15 m B köşesinde 50 ° 'lik bir açı oluşur Göreceli yüksekliği yan c, çevre ve o üçgenin alanına göre hesaplayın çözüm Bu durumda iki tarafın önlemleri vardır
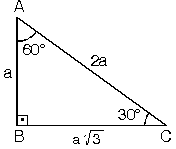



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Ucgenler Icin 76 Fikir Evde Egitim Matematik Egitim
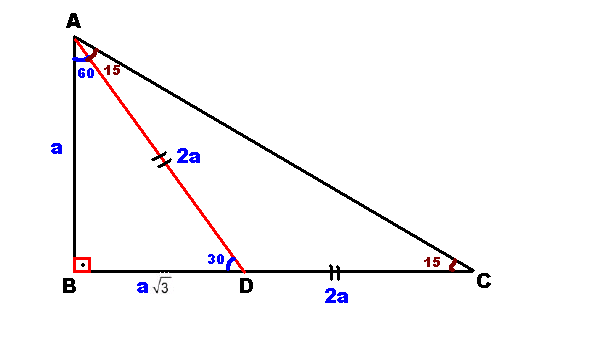
(15° – 75° – 90°) Üçgeni (15° – 75° – 90°) üçgeninde hipotenüse ait yükseklik AH = h dersek, Hipotenüs BC = 4h olur Hipotenüs kendisine ait yüksekliğin dört katıdır İKİZKENAR ÜÇGEN İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem açıortay, hem de kenarortaydır 1 15 75 90 üçgeni, üçgenler geometrinin temelini oluşturmaktadır Düzlemde doğrusal olmayan 3 noktanın birleşmesi ile oluşan geometrik şekildir Üç kenarı ve üç köşesi bulunan üçgenlerin 4 çeşidi bulunmaktadır Çeşitkenar üçgen, ikizkenar üçgen ve eşkenar üçgend Üçgeni Kenar Bağıntısı ( İSPAT ) tenten1 bu konuyu Geometri Formülleri forumunda açtı Cevap 2 Son mesaj 02 Ağu 13, 1933 üçgeni mrdanqerous bu konuyu Özel geometri soruları forumunda açtı Cevap 2 Son mesaj 18 Kas 12, 1806 ABC üçgeni




15 75 90 Ucgeni Pow Bylge
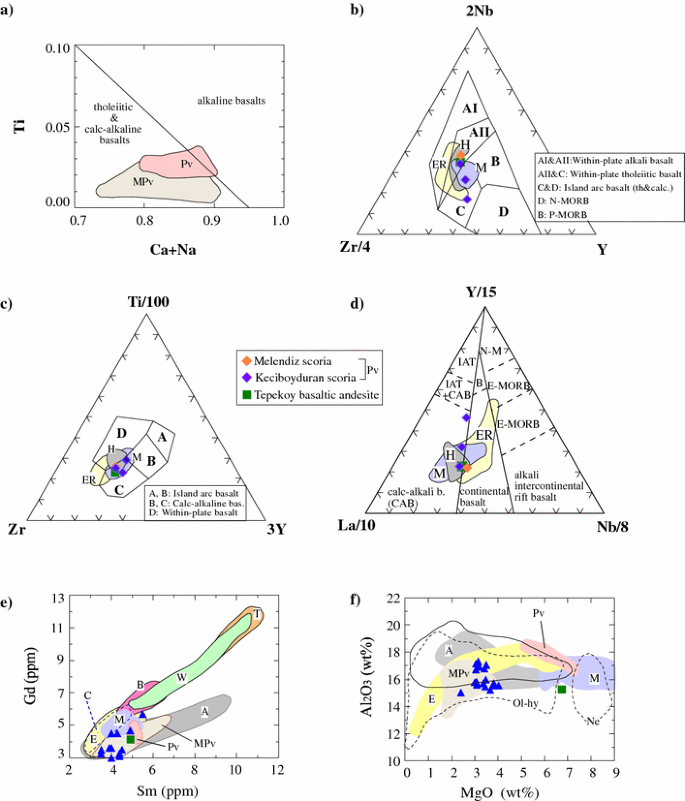



Review Of Post Collisional Volcanism In The Central Anatolian Volcanic Province Turkey With Special Reference To The Tepekoy Volcanic Complex Springerlink
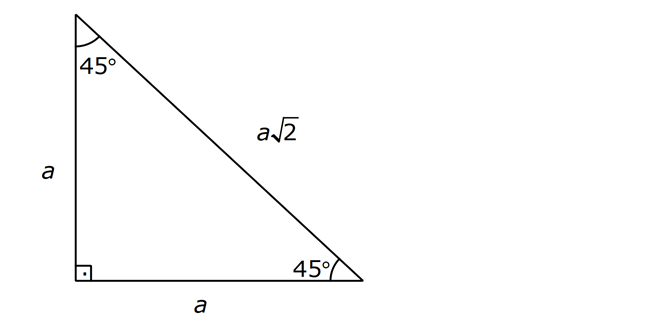
(15 75 90) Üçgeni (15 75 90) Üçgeni konusunu önce anlatıyoruz hemen ardından etkileşime geçmesini sağlıyoruz Bu şekilde kalıcılığı ve öğrenmeyi sağlıyoruzDik açılı üçgenlerin özellikleri Bir açısının ölçüsü 90°'ir 90°'nin karşısındaki kenar hipotenüstür ve diğer kenarlar dik kenarlardır;Hayyam Üçgeni Özellikleri (Posteri) yorum ve fiyatını inceleyin Hayyam Üçgeni Özellikleri (Posteri) en uygun fiyat ve hızlı kargo avantajıyla sahip olabilirsiniz Hayyam Üçgeni Özellikleri (Posteri) yorum ve fiyatını inceleyin Sipariş ve Destek 0850 840 78 16 0346 241 42 42



Dik Ucgen Ozellikleri Nelerdir




Dortgen Vikipedi Cute766
Dik Üçgenin Özellikleri Bir açısının ölçüsü 90° olan üçgene dik üçgen denir Dik üçgende 90° nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir Hipotenüs üçgenin daima en uzun kenarıdır şekilde, m (A) = 90° BC kenarı hipotenüs AB ve AC kenarları dik kenarlardırHipotenüs üçgenin en uzun kenarıdır;Bulunur ABE üçgeni (15 75 90 ) üçgenidir ABE üçgeninde E nin AB ye en yakın uzaklığı hipotenüse ait yükseklik;



1




Origin And Metamorphism Of Corundum Rich Metabauxites At Mt Ismail In The Southern Menderes Massif Sw Turkey Aydogan 12 Resource Geology Wiley Online Library
üçgeni 22,5 derecenin karşısındaki kenar " a " ise 67,5'un karşısındaki kenar " aakök2 " dir bir de hipotenüs ile ona ait yükseklik arasında bi bağıntı vardır hipotenüse ait yükseklik " h " ise hipotenüs " 2kök2h " dır düzgün sekizgende çok karşımıza çıkar düzgün bir sekizgenin en uzun veyaüçgeni Bu üçgende 15°'lik açının karşısındaki kenar 1 cm ise 75°'lik kenarın karşısındaki kenar 2 3 {\displaystyle 2 {\sqrt {3}}} cm olur İspatı ise 22,567,590 üçgenindeki gibidir Tek farkı, 75°'lik açının 15° ve 60°'lik açılara bölünmesidir Ayrıca bu(30 30 1) Üçgeni (15 75 90) Üçgeni (45 45 90) Üçgeni;
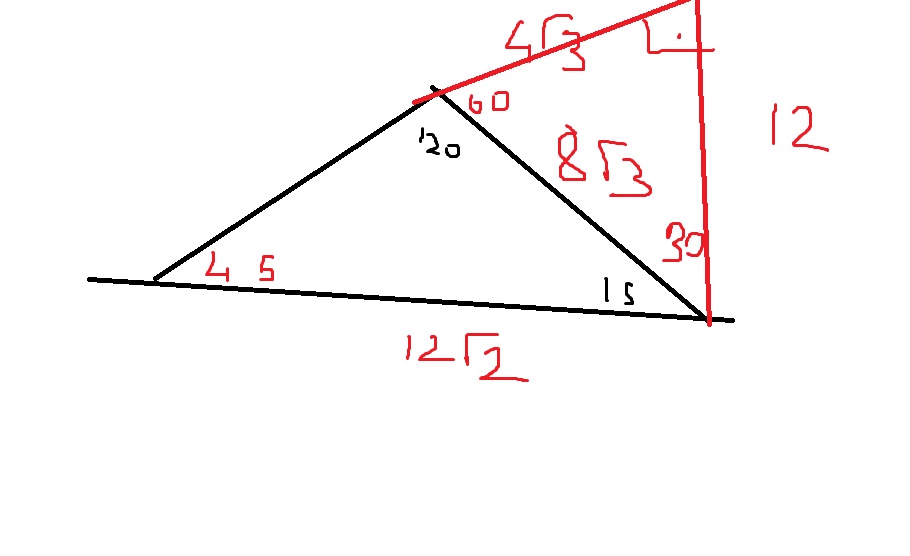



15 75 90 Ucgeni
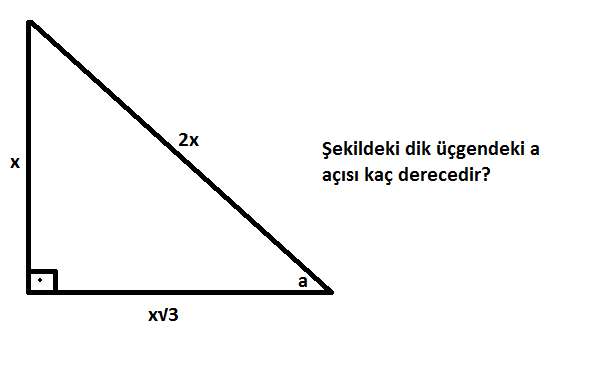



Acill Ozel Geometri Sorusu




Dik Ucgen 15 45 45 90 Ucgeni Evde Egitim Ders Calisma Ipuclari Matematik
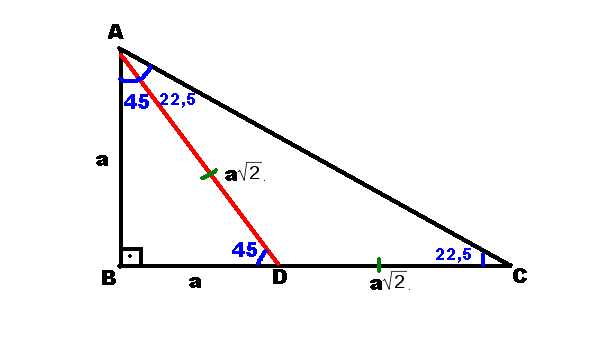



22 5 67 5 90 Ucgeni 1 2 Ispat




Ozel Ucgenler Not Bu
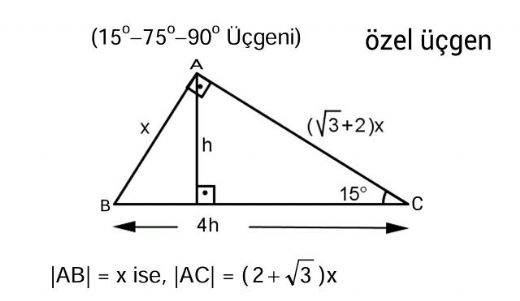



90 75 15 Ucgeni 90 75 15 Ucgeni Ozellikleri Ucgen Gen Tr




Dik Ucgen 17 22 5 67 5 90 Ucgeni Ders Calisma Ipuclari Evde Egitim Matematik




The Geochemical Composition Of The Palu Formation From The Palu Uluova Basin Elazig Eastern Anatolia Turkey Implication Of Source Area Weathering And Tectonic Setting Sciencedirect




15 75 90 Ucgeni Ispat Youtube




Ucgen Ve Ozellikleri Pisagor Arican Fen Bilimleri Facebook




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz
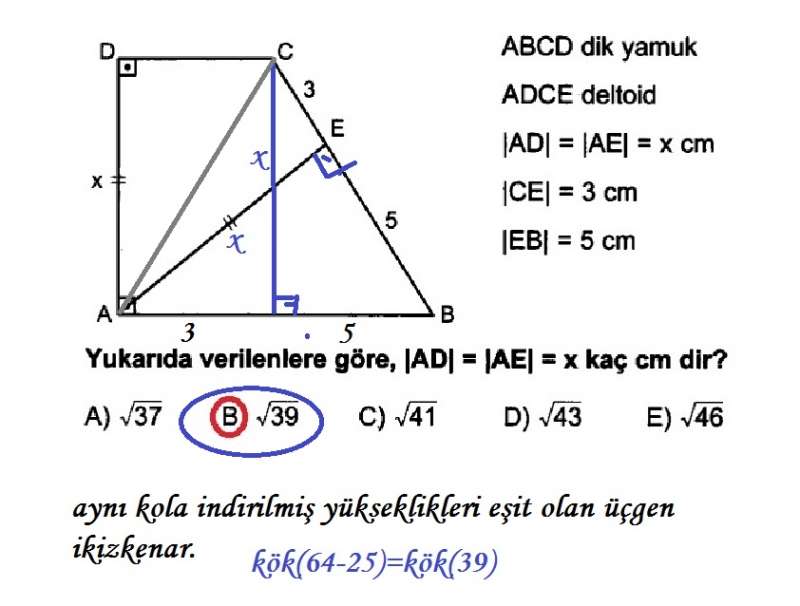



Yamuk




Dik Acili Ucgenlerin Ozellikleri Nelerdir Dik Ucgenlerin Temel Ozellikleri




15 75 90 Ucgeni Ucgende Acilar Ders Notlari Kunduz
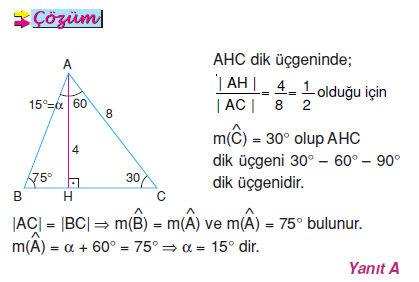



Dik Ucgen Konu Anlatimi Bilgicik Com Bilgicik Com
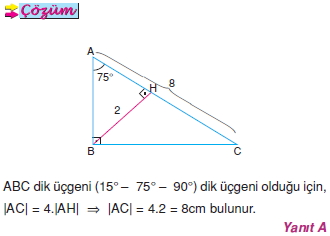



Ozellik 5 Bilgicik Com Bilgicik Com




15 75 90 Ucgeni Kurali Nedir 15 75 90 Ozel Ucgeni Ozellikleri Ve Ornek Sorular Egitim Haberleri




Ucgenler Ozel Ozel Ucgenler Ucgen Cesitleri Ucgenlerin Ozellikleri Pisagor Bagintisi Ile Ilgili Konu Anlatimlar Matematik Dersi Ile Ilgili Konu Anlatimlar Ornekler Cozumlu Sorular




lurplvgm7frm




Dik Ucgen 16 15 75 90 Ucgeni Temel Matematik Evde Egitim Matematik Felsefesi
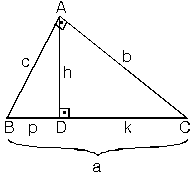



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir



Matematik Ogrenebilir Ppt Indir



Ozel Ucgenler Konu Anlatimi



ベスト 75 15 90 Ucgeni Ozellikleri シモネタ




Late Jurassic Magmatism And Stratigraphy In The Eastern Sakarya Zone Turkey Evidence For The Slab Breakoff Of Paleotethyan Oceanic Lithosphere The Journal Of Geology Vol 125 No 1




15 75 90 Ucgeni Webders Net



15 75 90 Ucgeni 2 3 Ispat
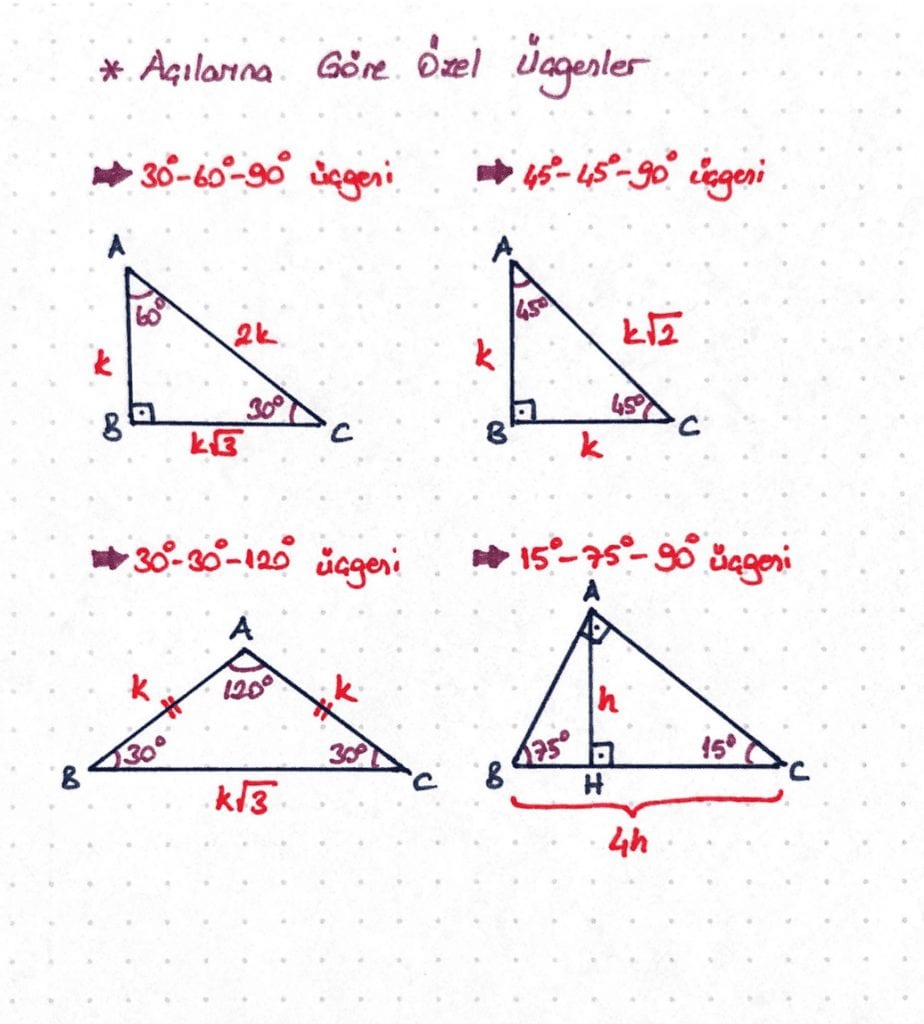



Ozel Ucgende Acilar



45 45 90 Ucgeni Matematikce




15 75 90 Ucgeni Akilli Geometri




Dik Ve Ozel Ucgenler 1
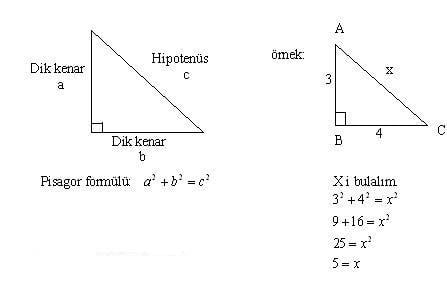



Dik Acili Ucgenin Kenar Ve Aci Ozellikleri Nedir




Ozel Ucgenler Ders Notu Konu Anlatimi Ders Notu




15 75 90 Ucgeni Ozellikleri Ve Kurali Ogrenci Yardim




Ozel Ucgenler Nelerdir Ozel Ucgenler 8 15 17 7 24 25 30 60 90 Ve Diger




Geochemistry Of The Middle Jurassic Sediments In Gumushane North Eastern Turkey Implications For Weathering And Provenance Saydam Eker Geological Journal Wiley Online Library




15 75 90 Ucgeni Ozellikleri Ve Kurallari




Dik Ucgen 6 15 75 90 Ucgeni Geometri Metin Hocam Youtube
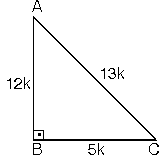



Dik Ve Ozel Ucgenler 1
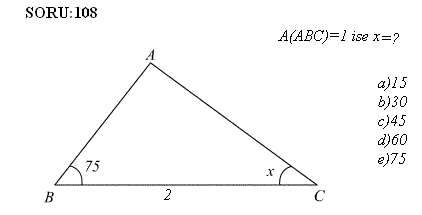



75 Li Bir Ucgen




Geometri Formulleri Sezgin Oner Matematik Yayinlari Facebook



Www Nanomatematik Com Wp Content Uploads 21 03 7 Sinif 5 Unite Birlestirilmis Matematik Pdf




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali




15 75 90 Ucgeni Ozellikleri Ve Kurali Soru List



9 Sinif Geometri Konu Ozeti Pdf Ucretsiz Indirin



Ozel Ucgenler Ozel Ucgenler Icindekiler Pisagor Bagintisi Oklit Bagintilari Kenarlarina Gore Ucgenler Acilarina Gore Ucgenler Kazanimlar Kaynakca Ppt Video Online Indir



15 75 90 Ucgeni Ozelliklerinin Ispati Youtube



Ozel Ucgenler Ppt Video Online Indir



15 75 90 Ucgeni Turleri Ve Ozellikleri




Dik Ucgen Wikiwand




135 30 15 Ucgenini Aciklayabilir Misiniz Eodev Com



Dergipark Org Tr En Download Article File 0350




15 75 90 Ucgeni Ozelliklerinin Ispati Ozeldersci



最高75 15 90 Ucgeni Kurali 最高のぬりえ




Ucgenin Alani Nasil Bulunur Ucgen Alan Formulleri Ve Cesitleri Bilgeniz Com



15 75 90 Ucgeni Uludag Sozluk




Dik Ucgen Formulleri



1



15 75 90 Ucgeni




Dershane Osym Lys Ygs Video Ders Konu Anlatim Izle On The App Store




Dik Ucgenler Pisagor Teoremi Konu Anlatimi Soru Cozumleri Ders Notu 9 Sinif Matematik Tyt




Dik Ucgen Konu Anlatimi Ve Ornek Soru Cozumu Kunduz



3
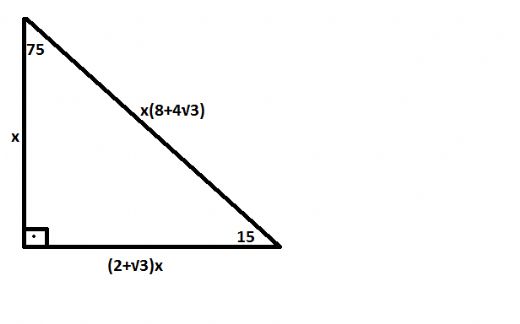



15 75 90 Ucgeninin Ozellikleri Nelerdir Ucgen Gen Tr




Ispat 15 75 90 Ucgeni Tyt Geometri Ozel Ucgenler Youtube




Dik Ucgen Oklid Bagintisi 30 60 90 Ucgeni Kurali
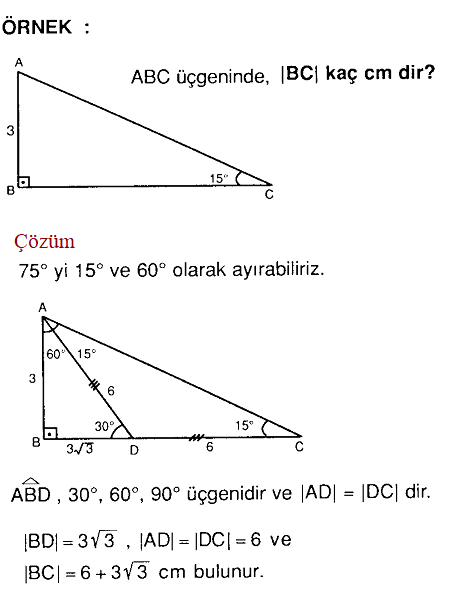



Net Fikir Dik Ucgen Ve Temel Ozellikleri




Acilarina Gore Ucgenler Ppt Indir




15 75 90 Ucgeni Not Bu



1




22 5 67 5 90 Ucgeni Ozelligi Matematik Ogretmenler Sarisin Renkli
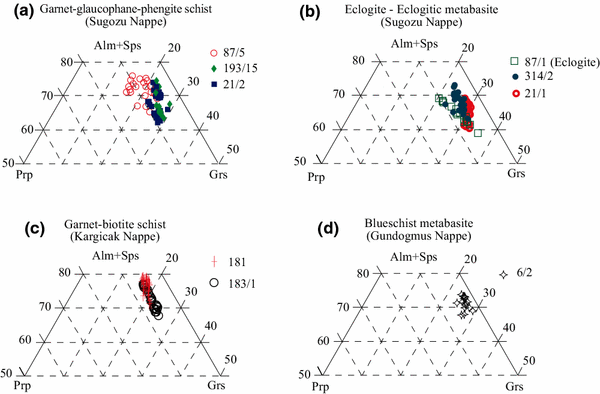



P T T Evolution Of Eclogite Blueschist Facies Metamorphism In Alanya Massif Time And Space Relations With Hp Event In Bitlis Massif Turkey Springerlink




15 75 90 Ucgen Ozelligi Ve 5 Ornek Cozum Youtube




Dik Ucgen Vikipedi



0 件のコメント:
コメントを投稿